|
Solutions pour la séance numéro 3 (énoncés)
|
 Retour à la page principale de
(gH)
Retour à la page principale de
(gH)
Module de Biostatistiques,
partie 1
Ecole Doctorale Biologie Santé
gilles.hunault "at" univ-angers.fr
Solutions pour la séance numéro 3 (énoncés)
Il existe bien sûr d'autres intervalles de confiance. Il y en a pour une variance (ce qui en fournit aussi un pour un écart-type), pour un rapport de cotes (odds ratio). Il y en a aussi pour une différence de proportions, pour une différence de moyennes, (avec des appariées ou non). Tous ces intervalles sont présentés dans le Triola.
Enfin, il y en a aussi pour un rapport de variances et pour un coefficient de corrélation linéaire. En fait, pratiquement à chaque test est associé un intervalle de confiance. On pourra s'en rendre compte avec par exemple les intructions R suivantes qui évitent de saisir des données pour "tester des tests":
example(cor.test) ----------------- cr.tst> ## Hollander & Wolfe (1973), p. 187f. cr.tst> ## Assessment of tuna quality. We compare the Hunter L measure of cr.tst> ## lightness to the averages of consumer panel scores (recoded as cr.tst> ## integer values from 1 to 6 and averaged over 80 such values) in cr.tst> ## 9 lots of canned tuna. cr.tst> cr.tst> x <- c(44.4, 45.9, 41.9, 53.3, 44.7, 44.1, 50.7, 45.2, 60.1) cr.tst> y <- c( 2.6, 3.1, 2.5, 5.0, 3.6, 4.0, 5.2, 2.8, 3.8) cr.tst> ## The alternative hypothesis of interest is that the cr.tst> ## Hunter L value is positively associated with the panel score. cr.tst> cr.tst> cor.test(x, y, method = "kendall", alternative = "greater") Kendall's rank correlation tau data: x and y T = 26, p-value = 0.05972 alternative hypothesis: true tau is greater than 0 sample estimates: tau 0.4444444 cr.tst> ## => p=0.05972 cr.tst> cr.tst> cor.test(x, y, method = "kendall", alternative = "greater", cr.tst+ exact = FALSE) # using large sample approximation Kendall's rank correlation tau data: x and y z = 1.6681, p-value = 0.04765 alternative hypothesis: true tau is greater than 0 sample estimates: tau 0.4444444 cr.tst> ## => p=0.04765 cr.tst> cr.tst> ## Compare this to cr.tst> cor.test(x, y, method = "spearm", alternative = "g") Spearman's rank correlation rho data: x and y S = 48, p-value = 0.0484 alternative hypothesis: true rho is greater than 0 sample estimates: rho 0.6 cr.tst> cor.test(x, y, alternative = "g") Pearson's product-moment correlation data: x and y t = 1.8411, df = 7, p-value = 0.05409 alternative hypothesis: true correlation is greater than 0 95 percent confidence interval: -0.02223023 1.00000000 sample estimates: cor 0.5711816 cr.tst> ## Formula interface. cr.tst> require(graphics) cr.tst> pairs(USJudgeRatings) cr.tst> cor.test(~ CONT + INTG, data = USJudgeRatings) Pearson's product-moment correlation data: CONT and INTG t = -0.8605, df = 41, p-value = 0.3945 alternative hypothesis: true correlation is not equal to 0 95 percent confidence interval: -0.4168591 0.1741182 sample estimates: cor -0.1331909 example(wilcox.test) -------------------- wlcx.t> require(graphics) wlcx.t> ## One-sample test. wlcx.t> ## Hollander & Wolfe (1973), 29f. wlcx.t> ## Hamilton depression scale factor measurements in 9 patients with wlcx.t> ## mixed anxiety and depression, taken at the first (x) and second wlcx.t> ## (y) visit after initiation of a therapy (administration of a wlcx.t> ## tranquilizer). wlcx.t> x <- c(1.83, 0.50, 1.62, 2.48, 1.68, 1.88, 1.55, 3.06, 1.30) wlcx.t> y <- c(0.878, 0.647, 0.598, 2.05, 1.06, 1.29, 1.06, 3.14, 1.29) wlcx.t> wilcox.test(x, y, paired = TRUE, alternative = "greater") Wilcoxon signed rank test data: x and y V = 40, p-value = 0.01953 alternative hypothesis: true location shift is greater than 0 wlcx.t> wilcox.test(y - x, alternative = "less") # The same. Wilcoxon signed rank test data: y - x V = 5, p-value = 0.01953 alternative hypothesis: true location is less than 0 wlcx.t> wilcox.test(y - x, alternative = "less", wlcx.t+ exact = FALSE, correct = FALSE) # H&W large sample Wilcoxon signed rank test data: y - x V = 5, p-value = 0.01908 alternative hypothesis: true location is less than 0 wlcx.t> # approximation wlcx.t> wlcx.t> ## Two-sample test. wlcx.t> ## Hollander & Wolfe (1973), 69f. wlcx.t> ## Permeability constants of the human chorioamnion (a placental wlcx.t> ## membrane) at term (x) and between 12 to 26 weeks gestational wlcx.t> ## age (y). The alternative of interest is greater permeability wlcx.t> ## of the human chorioamnion for the term pregnancy. wlcx.t> x <- c(0.80, 0.83, 1.89, 1.04, 1.45, 1.38, 1.91, 1.64, 0.73, 1.46) wlcx.t> y <- c(1.15, 0.88, 0.90, 0.74, 1.21) wlcx.t> wilcox.test(x, y, alternative = "g") # greater Wilcoxon rank sum test data: x and y W = 35, p-value = 0.1272 alternative hypothesis: true location shift is greater than 0 wlcx.t> wilcox.test(x, y, alternative = "greater", wlcx.t+ exact = FALSE, correct = FALSE) # H&W large sample Wilcoxon rank sum test data: x and y W = 35, p-value = 0.1103 alternative hypothesis: true location shift is greater than 0 wlcx.t> # approximation wlcx.t> wlcx.t> wilcox.test(rnorm(10), rnorm(10, 2), conf.int = TRUE) Wilcoxon rank sum test data: rnorm(10) and rnorm(10, 2) W = 6, p-value = 0.0003248 alternative hypothesis: true location shift is not equal to 0 95 percent confidence interval: -2.4667566 -0.8736843 sample estimates: difference in location -1.695926 wlcx.t> ## Formula interface. wlcx.t> boxplot(Ozone ~ Month, data = airquality) wlcx.t> wilcox.test(Ozone ~ Month, data = airquality, wlcx.t+ subset = Month %in% c(5, 8)) Wilcoxon rank sum test with continuity correction data: Ozone by Month W = 127.5, p-value = 0.0001208 alternative hypothesis: true location shift is not equal to 0 Message d'avis : In wilcox.test.default(x = c(41L, 36L, 12L, 18L, 28L, 23L, 19L, : cannot compute exact p-value with tiesOn trouvera dans l'article haukka.pdf des intervalles de confiance de prévalence (à ne pas confondre avec l'incidence) nommés bien sûr CI.
Si on utilise R Site Search pour chercher confidence and interval on trouve plusieurs milliers de résultats...
Les formules de calcul pour les intervalles de confiance reposent sur des hypothèses paramétriques de distribution, dont principalement l'utilisation de la loi normale de paramètres μ=0 et σ=1. On nomme petit échantillon un échantillon de taille inférieure à 50 (mais certains auteurs considérent un échantillon comme "non petit" à partir de 30 individus). Un échantillon normal est un échantillon dont les valeurs peuvent être considérées comme issues d'une loi normale. Il existe des tests de normalité qui ne s'appliquent en principe qu'à des échantillons de taille "suffisante". Sur la notion d'échantillon en général, voir sample (wiki US) et échantillon biaisé (wiki FR).
Il est important de savoir si un échantillon est petit ou non, normal ou non, parce qu'en fonction de ces caractéristiques, on utilise des statistiques de tests différentes. Ainsi l'intervalle de confiance d'une QT se calcule avec le test t de Student si l'échantillon est normal, avec le test de Wilcoxon si l'échantillon n'est pas normal.
Pour faire court : quand un échantillon est "très petit", on utilise un test non paramétrique. Sinon, quand l'échantillon est "grand" ou "normal", on utilise un test paramétrique ; quand il ne l'est pas, on utilise un test non paramétrique. Voir la page testscompar.htm pour une liste des tests possibles, paramétriques ou non.
Pour effectuer un test de normalité en R, on peut utiliser les fonctions shapiro.test et ks.test ou (plus avancé), le package nortest.
example(shapiro.test) ---------------------- shpr.t> shapiro.test(rnorm(100, mean = 5, sd = 3)) Shapiro-Wilk normality test data: rnorm(100, mean = 5, sd = 3) W = 0.9793, p-value = 0.1169 shpr.t> shapiro.test(runif(100, min = 2, max = 4)) Shapiro-Wilk normality test data: runif(100, min = 2, max = 4) W = 0.9322, p-value = 6.648e-05 example(ks.test) ---------------- ks.tst> require(graphics) ks.tst> x <- rnorm(50) ks.tst> y <- runif(30) ks.tst> # Do x and y come from the same distribution? ks.tst> ks.test(x, y) Two-sample Kolmogorov-Smirnov test data: x and y D = 0.52, p-value = 3.885e-05 alternative hypothesis: two-sided ks.tst> # Does x come from a shifted gamma distribution with shape 3 and rate 2? ks.tst> ks.test(x+2, "pgamma", 3, 2) # two-sided, exact One-sample Kolmogorov-Smirnov test data: x + 2 D = 0.2831, p-value = 0.0004875 alternative hypothesis: two-sided ks.tst> ks.test(x+2, "pgamma", 3, 2, exact = FALSE) One-sample Kolmogorov-Smirnov test data: x + 2 D = 0.2831, p-value = 0.0006614 alternative hypothesis: two-sided ks.tst> ks.test(x+2, "pgamma", 3, 2, alternative = "gr") One-sample Kolmogorov-Smirnov test data: x + 2 D^+ = 0.0673, p-value = 0.6086 alternative hypothesis: the CDF of x lies above the null hypothesis ks.tst> # test if x is stochastically larger than x2 ks.tst> x2 <- rnorm(50, -1) ks.tst> plot(ecdf(x), xlim=range(c(x, x2))) ks.tst> plot(ecdf(x2), add=TRUE, lty="dashed") ks.tst> t.test(x, x2, alternative="g") Welch Two Sample t-test data: x and x2 t = 5.216, df = 88.903, p-value = 5.911e-07 alternative hypothesis: true difference in means is greater than 0 95 percent confidence interval: 0.6523347 Inf sample estimates: mean of x mean of y -0.06534519 -1.02278526 ks.tst> wilcox.test(x, x2, alternative="g") Wilcoxon rank sum test with continuity correction data: x and x2 W = 1918, p-value = 2.096e-06 alternative hypothesis: true location shift is greater than 0 ks.tst> ks.test(x, x2, alternative="l") Two-sample Kolmogorov-Smirnov test data: x and x2 D^- = 0.48, p-value = 9.93e-06 alternative hypothesis: the CDF of x lies below that of yVoici les instructions R pour les calculs et les graphiques :
# lecture des données avec les fonctions standard de R url <- "http://forge.info.univ-angers.fr/~gh/wstat/Eda/choldata.dar" chol <- read.table(url,head=TRUE,row.names=1) # lecture des données avec les fonctions de statgh.r source("http://forge.info.univ-angers.fr/~gh/wstat/statgh.r",encoding="latin1") chol <- lit.dar(url) attach(chol) # description des données decritQT("Cholestérol",CHOLESTEROL,"g/l",TRUE) # tests de normalité print( ks.test(CHOLESTEROL,"pnorm",mean=mean(CHOLESTEROL),sd=sd(CHOLESTEROL)) ) print( shapiro.test(CHOLESTEROL) ) # test de conformité à la moyenne attendue print(t.test(CHOLESTEROL,mu=2.0)) # "libération" des données detach(chol)Et leurs résultats :
VARIABLE Cholestérol Taille 150 individus Moyenne 1.8200 g/l Ecart-type 0.3200 g/l Coef. de variation 18 % 1er Quartile 1.592 g/l Mediane 1.831 g/l 3eme Quartile 2.056 g/l iqr 0.4638 g/l Minimum 1.089357 g/l Maximum 2.674613 g/l Tracé tige et feuilles (the decimal point is 1 digit(s) to the left of the |) 10 | 9 11 | 0688 12 | 25 13 | 123455667 14 | 111445678 15 | 00015577888999 16 | 0011345578 17 | 122344555666677899 18 | 0000123334555556678899 19 | 001223344444778899 20 | 1234467778889 21 | 0011223444488 22 | 22345689 23 | 019 24 | 02 25 | 047 26 | 7 One-sample Kolmogorov-Smirnov test data: CHOLESTEROL D = 0.0485, p-value = 0.8717 alternative hypothesis: two-sided Shapiro-Wilk normality test data: CHOLESTEROL W = 0.9941, p-value = 0.7995 One Sample t-test data: CHOLESTEROL t = -6.8662, df = 149, p-value = 1.663e-10 alternative hypothesis: true mean is not equal to 2 95 percent confidence interval: 1.768198 1.871802 sample estimates: mean of x 1.82L'analyse des valeurs via le diagramme tige et feuilles ainsi que l'histogramme des classes semble indiquer que la distribution des données est à peu près normale et symétrique, ce que confirment les tests de normalité de Kolmogorov-Smirnov (p=0.87), le test de Shapiro (p=0.80) et le peu de différence entre la moyenne (1,82 g/l) et la médiane (1,83 g/l). Le troisième quartile (2.1 g/l) semble indiquer que de nombreuses valeurs sont inférieures ou égales à 2 g/l.
On prend comme hypothèse nulle qu'il n'y a pas de différence entre la moyenne de la population sous-jacente et la moyenne théorique de 2 g/l et comme hypothèse alternative que ces moyennes sont différentes (test bilatéral). Compte tenu de la normalité de la distribution, on utilise le test t de Student qui montre qu'il y a une différence significative (p=1.663e-10). On en conclut qu'au seuil de 1 % on peut rejeter l'hypothèse nulle c'est-à-dire qu'on peut considérer que la moyenne de la population est très significativement différente de 2 g/l.
Avec l'instruction R t.test(CHOLESTEROL,mu=2.0,alternative="less") on réalise un test unilatéral qui permet de tester si la moyenne est significativement inférieure à 2 g/l, ce qui est le cas ici (p= 8.316e-11).
Si vous éprouvez quelques difficultés à rédiger les hypothèses et leur conclusion, la lecture du cours de Christian Jost pour les statistiques de comparaison sur les données comportementales pourra vous aider (copie locale ici).
Voici une solution possible :
# du format large au format long n1 <- length(AGEH) n2 <- length(AGEF) AGE <- c(AGEH,AGEF) GROUPE <- rep( c(1,2), c(n1,n2) ) # du format long au format large AGEH <- AGE[ GROUPE==1 ] AGEF <- AGE[ GROUPE==2 ]Voici une première solution sous R avec certaines de nos fonctions :
# fonctions (gH) source("http://forge.info.univ-angers.fr/~gh/wstat/statgh.r",encoding="latin1") # lecture des données url <- "http://forge.info.univ-angers.fr/~gh/wstat/Eda/souris.dar" sou <- lit.dar(url) attach(sou) # analyse séparée des deux séries QT decritQT("Souche 1",SOUCHE1,"g/l",TRUE,"souche1.png") decritQT("Souche 2",SOUCHE2,"g/l",TRUE,"souche2.png") # conversion des 2 colonnes QT en # une colonne QT et une colonne QL (facteur) souris <- col2fact(cbind(SOUCHE1,SOUCHE2)) colnames(souris) <- c("marqueur","souche") # analyse par facteur decritQTparFacteur("Marqueur",souris[,1],"g/l","Souche ", souris[,2] ,"1 2",TRUE,"souris.png") # comparaison de moyennes compMoyData("Deux souches","SOUCHE1",SOUCHE1,"SOUCHE2",SOUCHE2) # libération des données detach(sou)Ci-dessous leurs résultats et les graphiques correspondants :
VARIABLE Souche 1 VARIABLE Souche 2 Taille 50 individus Taille 50 individus Moyenne 0.3000 g/l Moyenne 0.3200 g/l Ecart-type 0.0500 g/l Ecart-type 0.0100 g/l Coef. de variation 17 % Coef. de variation 3 % 1er Quartile 0.2654 g/l 1er Quartile 0.3125 g/l Mediane 0.3016 g/l Mediane 0.3203 g/l 3eme Quartile 0.3334 g/l 3eme Quartile 0.3269 g/l iqr 0.06805 g/l iqr 0.01438 g/l Minimum 0.1971346 g/l Minimum 0.2968209 g/l Maximum 0.4195308 g/l Maximum 0.3441783 g/l VARIABLE QT Marqueur unité : g/l VARIABLE QL Souche labels : 1 2 N Moy Unite Ect Cdv Q1 Med Q3 EIQ Min Max Global 100 0.3100 g/l 0.0374 12 0.3009 0.316 0.3284 0.02742 0.1971346 0.4195308 Souche 1 50 0.3000 g/l 0.0500 17 0.2654 0.3016 0.3334 0.06805 0.1971346 0.4195308 Souche 2 50 0.3200 g/l 0.0100 3 0.3125 0.3203 0.3269 0.01438 0.2968209 0.3441783 Analysis of Variance Table Response: nomVarQT Df Sum Sq Mean Sq F value Pr(>F) nomVarQL 1 0.010000 0.010000 7.5388 0.007185 ** Residuals 98 0.129994 0.001326 --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 COMPARAISON DE MOYENNES (valeurs fournies) : Deux souches Variable NbVal Moyenne Variance Ecart-type Cdv SOUCHE1 50 0.300 0.003 0.051 17 % SOUCHE2 50 0.320 0.000 0.010 3 % Global 100 0.310 0.001 0.038 12 % différence réduite : 2.7457 ; p-value 0.008231804 au seuil de 5 % soit 1.96, on peut rejeter l'hypothèse d'égalité des moyennes. En d'autres termes, il y a une différence significative entre les moyennes au seuil de 5 %. Voici ce qu'affiche la fonction t.test de R : Welch Two Sample t-test data: varA and varB t = -2.7457, df = 52.913, p-value = 0.008232 alternative hypothesis: true difference in means is not equal to 0 95 percent confidence interval: -0.034610715 -0.005389297 sample estimates: mean of x mean of y 0.30 0.32
On peut en conclure que les données semblent suivre à peu près une loi normale, qu'elles sont approximativement unimodales et sans valeur extrême. Les moyennes semblent peu différentes (0,30 vs 0,32) avec des variances comparables (0,05 vs 0,01). Le test de Welch va à l'encontre de l'intuition puisqu'il affirme que la différence entre les deux variables est significative (p=0,008).
Remarque : dans statgh.r il y a aussi une fonction nommée compare2QT ; on aurait pu l'utiliser ainsi, ce qui est plus "prudent" qu'avec les fonctions précédentes :
# lecture des données url <- "http://forge.info.univ-angers.fr/~gh/wstat/Eda/souris.dar" sou <- lit.dar(url) attach(sou) # utilisation de la fonction de comparaison compare2QT("souris : souche 1 vs souche 2", "souche 1",SOUCHE1,"souche 2",SOUCHE2,"g/l",TRUE) # libération des données detach(sou)En voici les résultats :
Shapiro-Wilk normality test data: varQt1 W = 0.9856, p-value = 0.7981 Shapiro-Wilk normality test data: varQt2 W = 0.9857, p-value = 0.8008 F test to compare two variances data: varQt1 and varQt2 F = 25.004, num df = 49, denom df = 49, p-value < 2.2e-16 alternative hypothesis: true ratio of variances is not equal to 1 95 percent confidence interval: 14.18916 44.06172 sample estimates: ratio of variances 25.00398 Welch Two Sample t-test data: varQt1 and varQt2 t = -2.7457, df = 52.913, p-value = 0.008232 alternative hypothesis: true difference in means is not equal to 0 95 percent confidence interval: -0.034610715 -0.005389297 sample estimates: mean of x 0.30 mean of y 0.32 Wilcoxon rank sum test with continuity correction data: varQt1 and varQt2 W = 910, p-value = 0.01926 alternative hypothesis: true location shift is not equal to 0 VARIABLE QT souris : souche 1 vs souche 2 unité : g/l VARIABLE QL Groupes labels : souche 1 souche 2 N Moy Unite Ect Cdv Q1 Med Q3 EIQ Min Max Global 100 0.3100 g/l 0.0374 12 0.3009 0.316 0.3284 0.02742 0.1971346 0.4195308 souche 1 50 0.3000 g/l 0.0500 17 0.2654 0.3016 0.3334 0.06805 0.1971346 0.4195308 souche 2 50 0.3200 g/l 0.0100 3 0.3125 0.3203 0.3269 0.01438 0.2968209 0.3441783 Analysis of Variance Table Response: nomVarQT Df Sum Sq Mean Sq F value Pr(>F) as.factor(nomVarQL) 1 0.010000 0.010000 7.5388 0.007185 ** Residuals 98 0.129994 0.001326 --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Les test de normalité effectués confirment que les distributions des variables peuvent être considérées comme normales (p=0,798 pour SOUCHE1 et p=0,800 pour SOUCHE2) ; le test F de Fisher pour les variances montre qu'on ne peut pas les considérer comme égales (p<2,2e-16), ce qui interdit d'utiliser le test paramétrique de Welch avec l'hypothèse d'égalité des variances. Le test non paramétrique de Wilcoxon indique également qu'il y a une différence significative entre les les deux variables (p=0,019).
Si on avait voulu les représentations en tige et feuilles en mode synoptique (voir ci-dessous), il aurait fallu : "bricoler" un peu les sorties fournies par R :
> stem(SOUCHE1) > stem(SOUCHE2) The decimal point is 2 digit(s) The decimal point is 2 digit(s) to the left of the | to the left of the | 18 | 7 20 | 7 22 | 5713588 24 | 36 26 | 2560368 29 | 7 28 | 01245 30 | 458889999 30 | 0123452 31 | 22234455666688 32 | 1226922479 32 | 0111234455566788889 34 | 4018 33 | 02359 36 | 4918 34 | 24 38 | 2 40 | 42 | 0Si on suppose que les données sont appariées, c'est-à-dire si on suppose que la donnée numéro i de la souche 1 est liée à la donnée numéro i de la souche 2, il faut ajouter l'option paired=TRUE dans l'expression pour le test paramétrique, soit :
> t.test(SOUCHE1,SOUCHE2) Welch Two Sample t-test data: SOUCHE1 and SOUCHE2 t = -2.7457, df = 52.913, p-value = 0.008232 alternative hypothesis: true difference in means is not equal to 0 95 percent confidence interval: -0.034610715 -0.005389297 sample estimates: mean of x mean of y 0.30 0.32 > t.test(SOUCHE1,SOUCHE2,paired=TRUE) Paired t-test data: SOUCHE1 and SOUCHE2 t = -3.4885, df = 49, p-value = 0.001036 alternative hypothesis: true difference in means is not equal to 0 95 percent confidence interval: -0.03152116 -0.00847885 sample estimates: mean of the differences -0.02000001Ce test est "plus exigeant" que le test de base pour la comparaison des QT. Il montre que la différence est encore plus significative si on considère que les données sont appariées (p=0,001 vs p=0,008).
Le test non paramétrique de Wilcoxon a aussi une option pour l'appariement :
> wilcox.test(SOUCHE1,SOUCHE2) Wilcoxon rank sum test with continuity correction data: SOUCHE1 and SOUCHE2 W = 910, p-value = 0.01926 alternative hypothesis: true location shift is not equal to 0 > wilcox.test(SOUCHE1,SOUCHE2,paired=TRUE) Wilcoxon signed rank test with continuity correction data: SOUCHE1 and SOUCHE2 V = 320, p-value = 0.002213 alternative hypothesis: true location shift is not equal to 0Là encore, ce test montre que la différence est encore plus significative si on considère que les données sont appariées (p=0,0022 vs p=0,0192).
Le wiki anglais donne un lien sur le test de Welch dans sa page sur le test t de Student... Le test t est un concept général qui se décline en test t de Student, test t de Welch... suivant que les variances sont considérées comme égales ou non.
Voici quelques calculs sous R :
avant <- c(125, 130, 132, 135, 136, 138, 140, 145) apres <- c(127, 132, 133, 136, 139, 141, 145, 148) decritQT("Durée avant dopage",avant,"s",TRUE,"avant.png") decritQT("Durée après dopage",apres,"s",TRUE,"apres.png") # test sans appariement sans hypothèse d'égalité des variances print( t.test(avant,apres,var.equal=FALSE) ) # test sans appariement sous hypothèse d'égalité des variances print( t.test(avant,apres,var.equal=TRUE) ) # test avec appariement sous hypothèse d'égalité des variances print( t.test(avant,apres,paired=TRUE,var.equal=TRUE) ) # test avec appariement sans hypothèse d'égalité des variances print( t.test(avant,apres,paired=TRUE,var.equal=FALSE) ) # utilisation de notre fonction de comparaison compare2QTappariees("Durée de parcours","avant",avant, "après",apres,"s",TRUE,"labyrinthe.png")Ci-dessous leurs résultats et les graphiques correspondants :
VARIABLE Durée avant dopage VARIABLE Durée après dopage Taille 8 individus Taille 8 individus Moyenne 135.1250 s Moyenne 137.6250 s Ecart-type 5.7974 s Ecart-type 6.5562 s Coef. de variation 4 % Coef. de variation 5 % 1er Quartile 131.5 s 1er Quartile 132.8 s Mediane 135.5 s Mediane 137.5 s 3eme Quartile 138.5 s 3eme Quartile 142 s iqr 7 s iqr 9.25 s Minimum 125 s Minimum 127 s Maximum 145 s Maximum 148 s Tracés tige et feuilles The decimal point is 1 digit(s) to the right of the | 12 | 5 12 | 7 13 | 02 13 | 23 13 | 568 13 | 69 14 | 0 14 | 1 14 | 5 14 | 58 Welch Two Sample t-test data: avant and apres t = -0.7558, df = 13.793, p-value = 0.4625 alternative hypothesis: true difference in means is not equal to 0 95 percent confidence interval: -9.604647 4.604647 sample estimates: mean of x mean of y 135.125 137.625 Two Sample t-test data: avant and apres t = -0.7558, df = 14, p-value = 0.4623 alternative hypothesis: true difference in means is not equal to 0 95 percent confidence interval: -9.594663 4.594663 sample estimates: mean of x mean of y 135.125 137.625 Paired t-test data: avant and apres t = -5.4006, df = 7, p-value = 0.001008 alternative hypothesis: true difference in means is not equal to 0 95 percent confidence interval: -3.594608 -1.405392 sample estimates: mean of the differences -2.5 Paired t-test data: avant and apres t = -5.4006, df = 7, p-value = 0.001008 alternative hypothesis: true difference in means is not equal to 0 95 percent confidence interval: -3.594608 -1.405392 sample estimates: mean of the differences -2.5 Shapiro-Wilk normality test data: varQt1 W = 0.9968, p-value = 0.9999 Shapiro-Wilk normality test data: varQt2 W = 0.9833, p-value = 0.9774 F test to compare two variances data: varQt1 and varQt2 F = 0.7819, num df = 7, denom df = 7, p-value = 0.7537 alternative hypothesis: true ratio of variances is not equal to 1 95 percent confidence interval: 0.1565389 3.9055070 sample estimates: ratio of variances 0.7818975 Paired t-test data: varQt1 and varQt2 t = -5.4006, df = 7, p-value = 0.001008 alternative hypothesis: true difference in means is not equal to 0 95 percent confidence interval: -3.594608 -1.405392 sample estimates: mean of the differences -2.5 Wilcoxon signed rank test with continuity correction data: varQt1 and varQt2 V = 0, p-value = 0.01356 alternative hypothesis: true location shift is not equal to 0 VARIABLE QT Durée de parcours unité : s VARIABLE QL Groupes labels : avant après N Moy Unite Ect Cdv Q1 Med Q3 EIQ Min Max Global 16 136.3750 s 6.3134 5 132 136 140.2 8.25 125 148 avant 8 135.1250 s 5.7974 4 131.5 135.5 138.5 7 125 145 après 8 137.6250 s 6.5562 5 132.8 137.5 142 9.25 127 148 Analysis of Variance Table Response: nomVarQT Df Sum Sq Mean Sq F value Pr(>F) as.factor(nomVarQL) 1 25.00 25.00 0.5712 0.4623 Residuals 14 612.75 43.77
Si on ne fait pas très attention, on pourrait conclure rapidement que les données semblent normales et que le test paramétrique t indique que les variables ne sont pas très différentes, avec ou sans hypothèse d'égalité des variances (p=0,46).
Par contre, si on utilise le fait que les données sont appariées, le test paramétrique t montre que la différence entre les moyennes est très significative (p=0,001).
En fait, le diagramme des tiges et feuilles montre qu'il y a très peu de données : 8 valeurs pour l'échantillon. Comme il est difficile de savoir s'il y a normalité avec aussi peu de valeurs, seul le test non paramétrique de Wilcoxon pour données appariées est licite ici, qui montre que les données sont significativement différentes (p=0,01).
Le risque de confusion est lié à l'apprentissage induit par le premier parcours du labyrinthe. Sauf à savoir (par un fait démontré) qu'un seul parcours de labyrinthe ne suffit pas à une souris pour mémoriser le parcours, il est possible que les temps "après" soient meilleurs que les "avant" à cause de la mémorisation. Il pourrait y avoir confusion entre l'amélioration éventuelle due à la substance et celle due à la mémorisation.
Comme l'énoncé reste vague («comparer...»), le plus raisonnable est de réaliser un test bilatéral. Si l'énoncé avait indiqué tester l'amélioration du temps de parcours..., il aurait été judicieux de réaliser un test unilatéral. Dans les deux cas, l'hypothèse nulle aurait été la même.
L'adjectif «dopante» a sans doute été mis pour induire (mais sans le dire explicitement) qu'on «aimerait bien» qu'un test unilatéral soit réalisé. Toutefois, au vu des moyennes, le dopage est sans doute inexistant puisque les souris sont plus lentes après qu'avant ! La vérification du test unilatéral associé est laissé à la discrétion des lecteurs..
Voici la signification des sigles et leur traduction (il y a des liens sous les sigles et les définitions) :
On parle d'analyse de variance parce que c'est la technique pour comparer des moyennes. Une ANOVA pour deux groupes est équivalente à un test t de Student. Pour plus de deux groupes, une ANOVA est la généralisation de ce test, avec comme outil principal le rapport des variances inter et intra. On pourra lire en français la page 5-3.html et les démonstrations de AI ACCESS.
Après une ANOVA, si au moins un des groupes est différent des autres, il faut effectuer des tests de comparaisons multiples nommés encore tests post hoc pour tester quels groupes peuvent être considérés comme non significativement différents. Il y a de nombreux tests post hoc et ils ne servent pas tous à la même chose. On pourra lire la page d'aide de SPSS sur le sujet ou celle de SAS.
Voici les instructions R qui montrent l'équivalence entre l'ANOVA et le test t pour deux moyennes :
# lecture des données url <- "http://forge.info.univ-angers.fr/~gh/wstat/Eda/souris.dar" sou <- lit.dar(url) attach(sou) # conversion pour utiliser anova souris <- col2fact(cbind(SOUCHE1,SOUCHE2)) colnames(souris) <- c("marqueur","souche") # anova print( anova( lm(souris[,1] ~ souris[,2]) ) ) # test t print( t.test(SOUCHE1,SOUCHE2,var.equal=TRUE) ) detach(sou)Et leurs résultats :
Analysis of Variance Table Response: souris[, 1] Df Sum Sq Mean Sq F value Pr(>F) souris[, 2] 1 0.010000 0.010000 7.5388 0.007185 ** Residuals 98 0.129994 0.001326 --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Two Sample t-test data: SOUCHE1 and SOUCHE2 t = -2.7457, df = 98, p-value = 0.007185 alternative hypothesis: true difference in means is not equal to 0 95 percent confidence interval: -0.034455158 -0.005544854 sample estimates: mean of x mean of y 0.30 0.32Pour réaliser une ANOVA des données IRIS, variable petal.length en fonction de l'espèce, on peut utiliser le code suivant :
catss("ANOVA iris") # ANOVA minimale des données IRIS, variable petal.length en fonction de l'espèce anova(lm(iris$Petal.Length ~ iris$Species)) cats("détails") # calculs et tracés par groupes res <- data.frame( tapply(F=length,X=iris$Petal.Length,I=iris$Species) , tapply(F=mean,X=iris$Petal.Length,I=iris$Species) , tapply(F=median,X=iris$Petal.Length,I=iris$Species) , tapply(F=sd,X=iris$Petal.Length,I=iris$Species) ) names(res) <- c("nb","moy","med","ect") print(res) boxplot(iris$Petal.Length ~ iris$Species,col="yellow")On obtient alors
+ ========== + + + + ANOVA iris + + + + ========== + Analysis of Variance Table Response: iris$Petal.Length Df Sum Sq Mean Sq F value Pr(>F) iris$Species 2 437.10 218.551 1180.2 < 2.2e-16 *** Residuals 147 27.22 0.185 --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 détails ======= nb moy med ect setosa 50 1.462 1.50 0.1736640 versicolor 50 4.260 4.35 0.4699110 virginica 50 5.552 5.55 0.5518947
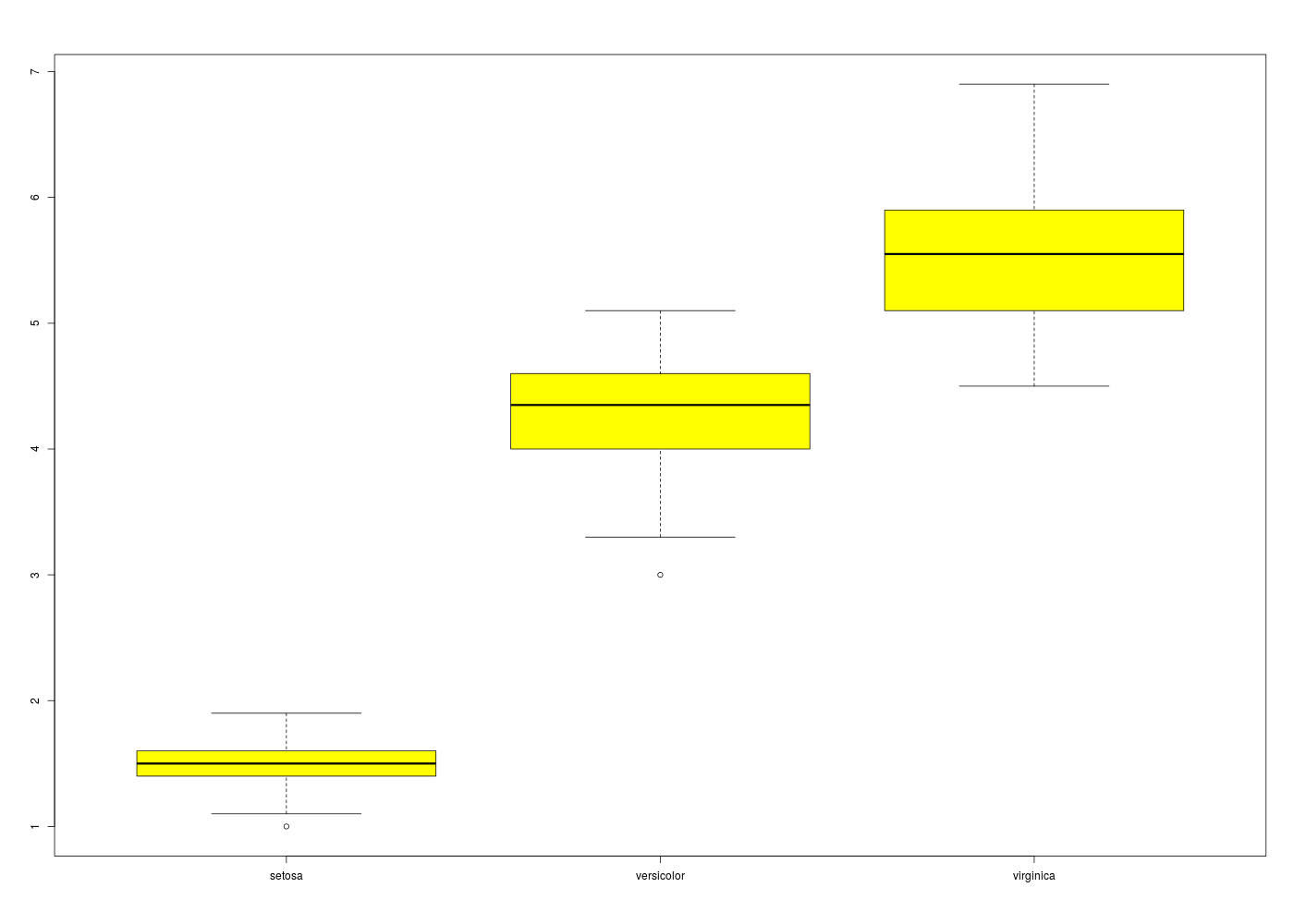
Il reste à expliciter ce qu'on en déduit et effectuer ici des tests post hoc...Voici par exemple l'utilisation de la fonction pairwise.t.test() qui montre ici que les trois espèces peuvent être considérées comme distinctes au niveau de la longueur des pétales :
> pairwise.t.test(iris$Petal.Length,g=iris$Species) Pairwise comparisons using t tests with pooled SD data: iris$Petal.Length and iris$Species setosa versicolor versicolor <2e-16 - virginica <2e-16 <2e-16 P value adjustment method: holmIl suffit d'utiliser le test avec des données dont on connait le résultat du test. Par exemple pour une comparaison de moyennes, il suffit de prendre des données très proches et des données très éloignées pour vérifier comment fonctionne la p-value. En voici un exemple :
cat("# données presque identiques, la p-value doit approcher 1\n") a <- rnorm(20) b <- a + rnorm(20)/150 print( t.test(a,b) ) cat("# données similaires, la p-value doit dépasser largement 0,05\n") a <- c(10,20,15,25,30,50,70,30) b <- a + c(1,2,5,2,3,5,7,3) print( t.test(a,b) ) cat("# données très différentes, la p-value est inférieure à 0,05\n") a <- c(10,20,15,25,30,50,70,30,8,2,1,10,8) b <- c(210,820,315,2500,310,450,170,230,5,350,10,3560) print( t.test(a,b) )Les résultats sont indiqués ci-dessous :
# données presque identiques, la p-value doit approcher 1 Welch Two Sample t-test data: a and b t = 0.0071, df = 38, p-value = 0.9944 alternative hypothesis: true difference in means is not equal to 0 95 percent confidence interval: -0.6686062 0.6733292 sample estimates: mean of x mean of y 0.2726208 0.2702594 # données similaires, la p-value doit dépasser largement 0,05 Welch Two Sample t-test data: a and b t = -0.3397, df = 13.914, p-value = 0.7391 alternative hypothesis: true difference in means is not equal to 0 95 percent confidence interval: -25.60781 18.60781 sample estimates: mean of x mean of y 31.25 34.75 # données très différentes, la p-value est inférieure à 0,05 Welch Two Sample t-test data: a and b t = -2.2515, df = 11.007, p-value = 0.04576 alternative hypothesis: true difference in means is not equal to 0 95 percent confidence interval: -1429.15923 -16.25103 sample estimates: mean of x mean of y 21.46154 744.16667En mathématiques, on étudie les fonctions et il y a des modèles comme les fonctions polynomes, les fonctions trigonométriques (directes, inverses, hyperboliques), les fonctions puissances, exponentielles, logarithmiques... dont les courbes représentatives sont nommées droites, paraboles, hyperboles, sinusoides... En statistiques, on étudie des fonctions nommées « variables aléatoires » (!) ou V.A. et les grandes familles de V.A. définissent des modèles probabilistes. Les V.A. sont définies sur des espaces probabilisés, eux-mêmes issus d'espaces probabilisables munis d'une probabilité.
On distingue classiquement les V.A. dont les valeurs sont au plus dénombrables (V.A. dites discrètes) des autres V.A. dites continues). Ainsi le modèle binomial, le modèle uniforme et le modèle poissonnien sont discrets, alors que le modèle gaussien est continu. Les fonctions de distribution, densité et répartition sont souvent nommées lois plutôt que modèles...
Le wiki français, sous la rubrique loi de probabilité est une référence mathématique seulement. Seul un cours détaillé et des exemples peuvent fournir le recul nécessaire à la compréhension de ces lois. En fin de page du wiki anglais, sous la rubrique probability distribution, on trouve des PDF qui recensent de nombreuses lois, dont DistributionsHandbook.pdf.
L'expression à calculer est :
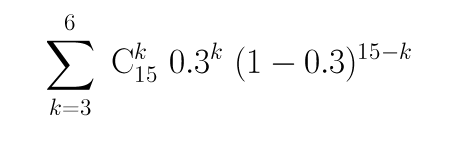
Sachant que "x puissance y" se calcule en R par "x ** y" et que le coefficient du binome Cnp s'obtient par choose(b,p) on peut calculer la probabilité demandée par :
n <- 15 p <- 0.3 q <- 1-p proba <- 0 for (k in (3:6)) { proba <- proba + choose(n,k)*(p**k)*(q**(n-k)) } # fin pour k print( proba )On obtient alors 0,7420297 (alors que la valeur exacte est plutôt 0,7419). Si on connait mieux R, on peut utiliser l'expression plus courte sum(dbinom(3:6,15,0.3)) qui renvoie bien sûr la même valeur numérique.
On calcule ensuite m=np=4.5 et s2=np(1-p)=3.15 d'où s=1.7748 et on passe de X=B(n,p) à (X-m)/s approximé par Y=N(μ=0,σ=1).
Sans la correction de continuité, on approxime 3≤X≤6 par (3-m)/s≤Y≤(6-m)/s soit -0,8451543≤Y≤0,8451543. Si F désigne la fonction de répartition de la loi normale, alors F(-y)=1-F(y) et donc p(-y≤Y≤y) vaut F(y)-F(-y)=2F(y)-1. Puisque F(y) se calcule sous R par pnorm(y), l'approximation de p(3≤=X≤6) est donc 2*pnorm(0.8451543)-1 soit à peu près 0,6019753.
Avec la correction de continuité, on approxime 3≤X≤6 par (2.5-m)/s≤Y≤(6.5-m)/s soit -1,126872≤Y≤1,126872. L'approximation demandée est alors donc 2*pnorm(1,126872)-1 soit à peu près 0,74020.
Cette approximation est "assez bonne" alors que les conditions d'application de l'approximation n>35, np>5 et nq>5 ne sont pas respectées (mais 4.5 n'est quand même pas très loin de 5).
Suite à l'exercice précédent, la valeur exacte demandée est sum(dbinom(0:1,n,p)) soit 0,5577417. L'approximation par la loi normale avec la correction de continuité et celle par la loi de Poisson se calculent comme suit :
# paramètres de la loi binomiale n <- 1500 p <- 1/1000 # moyenne et écart-type de la loi binomiale m <- n*p s <- sqrt(n*p*(1-p)) # valeur avec la correction de continuité : # B < 2 devient X < 1.5 x <- 2 - 0.5 # approximation par la loi normale centrée-réduite cat( "Approximation par N(0,1) : ",pnorm( (x-m)/s ),"\n" ) # approximation par la loi de Poisson # de même moyenne cat( "Approximation par P(",m,") : ",sum(dpois(0:1,m) ),"\n" )Voici ce qui est calculé :
Approximation par N( 0,1 ) : 0.5 Approximation par P( 1.5 ) : 0.5578254L'approximation par la loi normale n'est pas très bonne parce que les conditions d'application de l'approximation ne sont pas respectées. Pour la loi de Poisson, les conditions n>40 et np<5 sont respectées, d'où une meilleure approximation.
Le package TeachingDemos contient entre autres une jolie fonction nommée vis.binom() pour visualiser la loi binomiale.
Celui de Gael MILLOT, nommé Comprendre et réaliser les tests statistiques à l'aide de R mais attention : c'est un gros pavé de 704 pages dans un format presque A4, soit 1,73 kg, un gros pavé, quoi ! Heureusement, la moitié des droits d'auteur sont reversés à l'Institut Curie.
Pour une introduction à la régression sous R, voir l'excellent numéro 35 (décembre 2006) de la revue MODULAD (MODULAD signifie « Le Monde des Utilisateurs de L'Analyse de Données »). Josiane CONFAIS et Monique LE GUEN y fournissent un tutoriel détaillé (140 pages) sur la régression linéaire, malheureusement (pour la pratique) en utilisant le logiciel SAS. Une copie locale du document est ici.
Pour une présentation succincte de la notion de régression (simple, multiple, linéaire, logistique...), voir notre séance 1 du module 2 : énoncé ; corrigé. Corrélation et causalité ne désignent pas la même chose : conceptuellement, si X et Y sont corrélées, il y a une liaison entre X et Y, sans notion de cause et d'effet. De plus, la corrélation linéaire est symétrique : Y = aX + b peut se réécrire X = cY + d. Alors que la causalité implique un sens, souvent exprimée avec X comme cause et Y comme effet.
Après élimination des lignes avec données manquantes, conversion en unités françaises, on peut montrer qu'il y a une corrélation linéaire entre POIDS et CEINTURE (ou plutôt tour de taille), mais pas entre POIDS et TAILLE :
# lecture du fichier des données diabetes <- lit.dar(""http://forge.info.univ-angers.fr/~gh/wstat/Eda/diabetes.dar") # on ne garde que l'identifiant, height, weight et waist hww_org <- diabetes[,c("height","weight","waist")] # "normalisation" du nom des lignes row.names(hww_org) <- paste("P",sprintf("%03d",as.numeric(row.names(diabetes))),sep="") # élimination des données avec NA hww <- na.omit(hww_org) # affichages cat("\n\nDonnées DIABETES, dimensions initiales",dim(diabetes),"\n\n") cat("\n\naprès suppression des données manquantes, données HW, dimensions ",dim(hww),"\n\n") cat("Début des données utilisées\n") print(head(hww)) cat("Fin des données utilisées\n") print(tail(hww)) # pour des français, il vaut mieux convertir les données # un pouce = 0,0254 m ; une livre = 0.45359237 kg poids <- hww$weight*0.45359237 taille <- hww$height*0.0254 ceinture <- hww$waist*2.54 # description élémentaire des variables decritQT("Taille",taille,"m" ,TRUE,"hw_taille.png") decritQT("Poids" ,poids ,"kg",TRUE,"hw_poids.png") decritQT("Ceinture" ,ceinture ,"cm",TRUE,"hw_ceint.png") # régression linéaire 1 anaLin("Taille",taille,"m" ,"Poids" ,poids ,"kg",TRUE,"hw_rl1.png") # régression linéaire 2 anaLin("Poids",poids,"kg" ,"Ceinture" ,ceinture ,"cm",TRUE,"hw_rl2.png") # détail "à la main" pour Ceinture = a*Poids + b rl <- lm(ceinture ~ poids) rho <- sprintf("%5.2f",cor(ceinture,poids)) vala <- sprintf("%.2f",rl$coefficients[2]) valb <- sprintf("%.2f",rl$coefficients[1]) titre <- paste("Ceinture = ",vala,"*Poids + ",valb," (rho = ",rho,")",sep="") gr("hw_rl3a.png") plot(ceinture ~ poids,main=titre,col="blue",pch=21,bg="blue",xlab="poids (kg) ",ylab="tour de taille (cm)") abline(rl,col="red") dev.off() # analyse graphqiue des résidus pour la régression Ceinture = a*Poids + b pdv <- 1:6 # plage de variation for (igr in pdv) { png(filename=paste("hw_rl3b_",igr,".png",sep=""),width=1024,height=768) plot(rl,which=igr,main=paste("Régression : ",titre)) dev.off() } # fin pour igrVoici ce qui est calculé :
Données DIABETES, dimensions initiales 403 19 après suppression des données manquantes, données HW, dimensions 395 3 Début des données utilisées height weight waist P001 62 121 29 P002 64 218 46 P003 61 256 49 P004 67 119 33 P005 68 183 44 P006 71 190 36 Fin des données utilisées height weight waist P398 61 115 31 P399 69 173 35 P400 63 154 32 P401 69 167 33 P402 63 197 41 P403 64 220 49 DESCRIPTION STATISTIQUE DE LA VARIABLE Taille Taille 395 individus Moyenne 1.6770 m Ecart-type 0.0996 m Coef. de variation 6 % 1er Quartile 1.6 m Mediane 1.676 m 3eme Quartile 1.753 m iqr absolu 0.1524 m iqr relatif 9 % Minimum 1.3208 m Maximum 1.9304 m Tracé tige et feuilles The decimal point is 1 digit(s) to the left of the | 13 | 2 13 | 14 | 02 14 | 777 15 | 0000000002222222222 15 | 55555555555555555557777777777777777777777777777777 16 | 0000000000000000000000000000000000000000000333333333333333333333333333333333 16 | 5555555555555555555555555555555588888888888888888888888888888888888 17 | 00000000000000000000000000000000000033333333333333333333333333 17 | 555555555555555555555555555555555555888888888888888888888888 18 | 000000000000000000000033333333333333 18 | 5555555588888 19 | 111133 DESCRIPTION STATISTIQUE DE LA VARIABLE Poids Taille 395 individus Moyenne 80.7096 kg Ecart-type 18.3062 kg Coef. de variation 23 % 1er Quartile 68.49 kg Mediane 78.47 kg 3eme Quartile 90.72 kg iqr absolu 22.23 kg iqr relatif 28 % Minimum 44.9056 kg Maximum 147.4175 kg Tracé tige et feuilles The decimal point is 1 digit(s) to the right of the | 4 | 556889 5 | 0012222224444444444445555666677777888999999 6 | 11122223333344444444455556666666666666677777888888899999 7 | 00000000111111222222222223333333333334444444455555555555566666666677777777777777777777888888899999999 8 | 00011111111111122222222222222333333333333334444444444455555556666666677777788999999 9 | 0000111111111222333333335555555556666677888889999 10 | 00001111122233334456677788 11 | 11123444566677899 12 | 01246689 13 | 112 14 | 057 vous pouvez utiliser hw_poids.png DESCRIPTION STATISTIQUE DE LA VARIABLE Ceinture Taille 395 individus Moyenne 96.3271 cm Ecart-type 14.5703 cm Coef. de variation 15 % 1er Quartile 83.82 cm Mediane 93.98 cm 3eme Quartile 104.1 cm iqr absolu 20.32 cm iqr relatif 22 % Minimum 66.0400 cm Maximum 142.2400 cm Tracé tige et feuilles The decimal point is 1 digit(s) to the right of the | 6 | 669 7 | 111111144444444444 7 | 666666666999999999999999999999 8 | 1111111111111111111114444444444444444444444444444 8 | 6666666666666666666666699999999999999999999 9 | 1111111111111111111111111444444444444444444444444444444444 9 | 777777777777777777777777777999999999999999999999999 10 | 222222222222222222222222222444444444444444444 10 | 7777777777777779999999999999999 11 | 22222222222244444444444 11 | 7777777779999999 12 | 222222224444444 12 | 777 13 | 000022 13 | 55 14 | 02 vous pouvez utiliser hw_ceint.png ANALYSE DE LA LIAISON LINEAIRE ENTRE Taille ET Poids coefficient de corrélation : 0.2492314 donc R2 = 0.06211628 p-value associée : 5.246671e-07 équation : Poids = 45.82 * Taille + 3.86 équation : Taille = 0.00 * Poids + 1.57 vous pouvez utiliser hw_rl1.png ANALYSE DE LA LIAISON LINEAIRE ENTRE Poids ET Ceinture coefficient de corrélation : 0.8509627 donc R2 = 0.7241375 p-value associée : 0 équation : Ceinture = 0.68 * Poids + 41.66 équation : Poids = 1.07 * Ceinture + -22.28Graphiques associés :
Pour réaliser une régression linéaire des données IRIS sur les variables petal.length et petal.width, on peut utiliser le code :
ml <- lm(Petal.Length ~ Petal.Width, data=iris) print(ml) plot(Petal.Length ~ Petal.Width, data=iris,type="p") abline(ml,col="red",lwd=2)Voici ce qui est calculé :
Call: lm(formula = Petal.Length ~ Petal.Width, data = iris) Coefficients: (Intercept) Petal.Width 1.084 2.230 Call: lm(formula = Petal.Length ~ Petal.Width, data = iris) Residuals: Min 1Q Median 3Q Max -1.33542 -0.30347 -0.02955 0.25776 1.39453 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 1.08356 0.07297 14.85 <2e-16 *** Petal.Width 2.22994 0.05140 43.39 <2e-16 *** --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Residual standard error: 0.4782 on 148 degrees of freedom Multiple R-squared: 0.9271, Adjusted R-squared: 0.9266 F-statistic: 1882 on 1 and 148 DF, p-value: < 2.2e-16
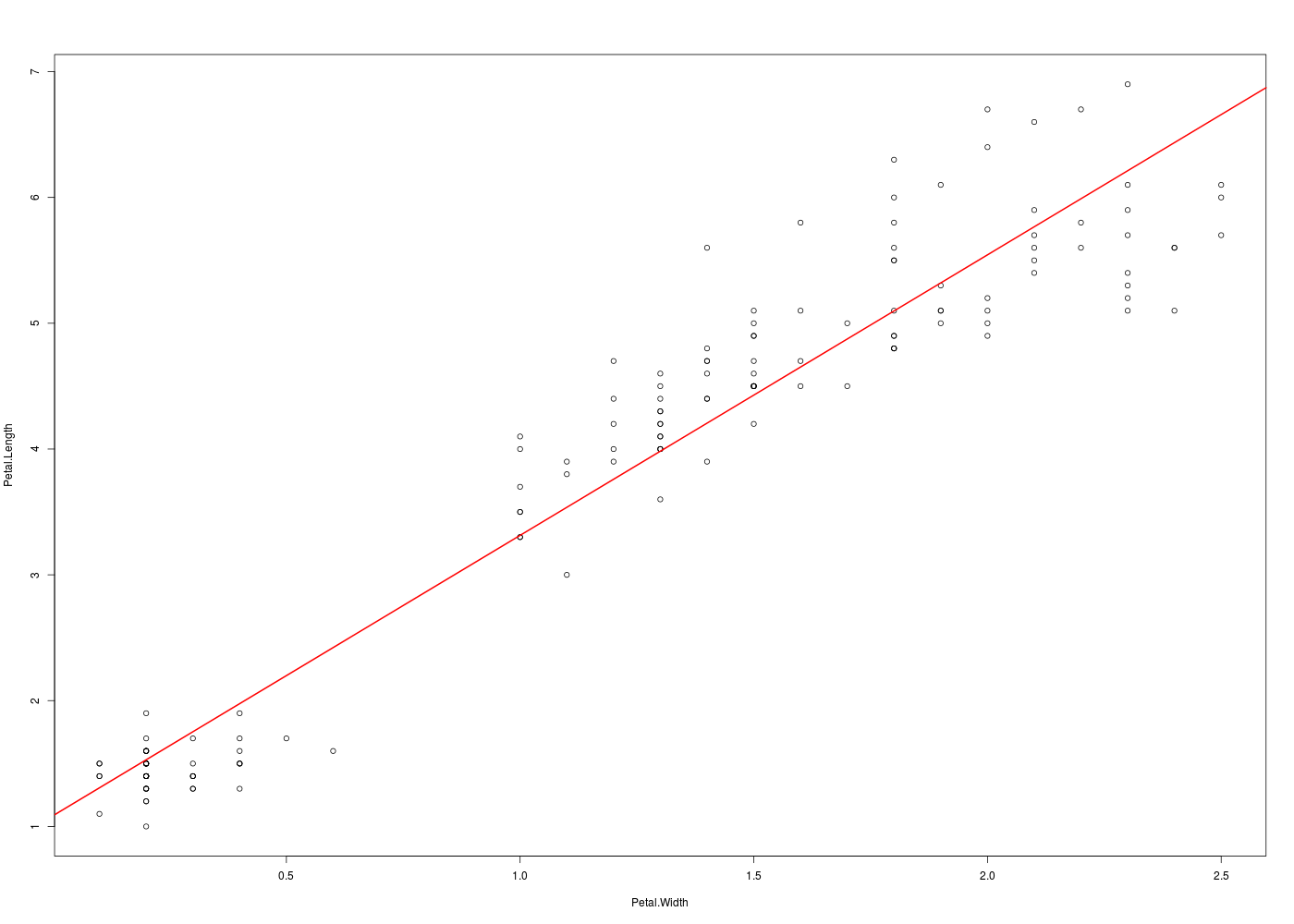
Il est clair que sans une rédaction détaillée ceci est incompréhensible....
Retour à la page principale de (gH)